Solution of Quadratic Equations
To find the solution set of a quadratic equation, following methods are used:
- factorization
- completing square
- use of quadratic formula
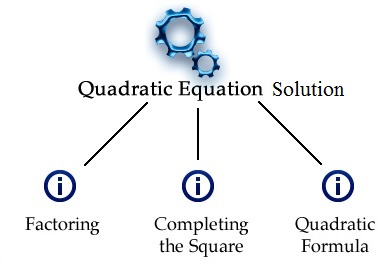
To find the solution set of a quadratic equation, following methods are used:
A body is said to be vibrating if it moves back and forth or to and fro about a point. Another term for vibration is oscillation. A special kind of vibratory or oscillatory motion is called the Simple Harmonic Motion (SHM). Simple Harmonic Motion (SHM) A body is said to be executing Simple Harmonic Motion…
Question 1. Find the order of the following matrices. Solution: $$ A = \begin {bmatrix} 2 & 3 \\ -5 & 6 \\ \end{bmatrix} $$ Order of matrix A is 2-by-2 $$ B = \begin {bmatrix} 2 & 0 \\ 3 & 5 \\ \end{bmatrix} $$ Order of matrix B is 2-by-2 $$…
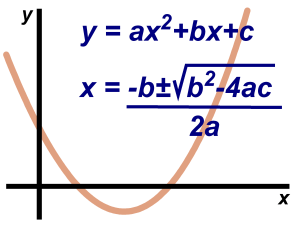
An equation of 2nd degree is called quadratic equation. In more detail, the quadratic equation is an equation, which contains the square of the unknown (variable) quantity, but no higher power. General or standard form of a quadratic equation: A 2nd degree equation in one variable x of the form as below, where a ≠ 0…

Hazrat Muhammad’s ﷺ life is a perfect model and example for the people who want to attain goodness, piety and success in their individual as well social life. People can seek light from the message and guidance from his life to achieve perfection in the moral, spiritual and social areas of life. He ﷺ has set very…
A set is a collection of well defined distinct objects or symbols. Well defined objects mean that the objects possess a property that enables one to determine whether a given object is in the collection or not. For example, a set cannot consist of elements like moral values, concepts, evils or virtues. Element of a…
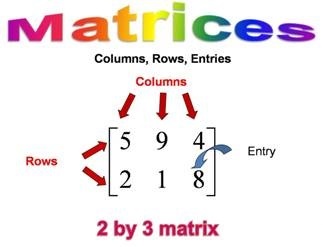
The matrices and determinants are used in the field of Mathematics, Physics, Statistics, Electronics and other branches of science. The matrices have played a very important role in this age of computer science. The idea of matrices was given by Arthur Cayley, an English mathematician of nineteenth century, who first developed, “Theory of Matrices” in…
You must be logged in to post a comment.