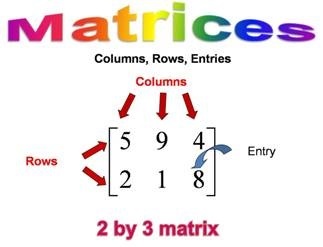
Question 1. Find the order of the following matrices.
Solution:
$$ A = \begin {bmatrix} 2 & 3 \\ -5 & 6 \\ \end{bmatrix} $$
Order of matrix A is 2-by-2
$$ B = \begin {bmatrix} 2 & 0 \\ 3 & 5 \\ \end{bmatrix} $$
Order of matrix B is 2-by-2
$$ C = \begin {bmatrix} 2 & 4 \\ \end{bmatrix} $$
Order of matrix C is 1-by-2
$$ D = \begin {bmatrix} 4 \\ 0 \\ 6 \\ \end{bmatrix} $$
Order of matrix D is 3-by-1
$$ E = \begin {bmatrix} a & d \\ b & e \\ c & f \\ \end{bmatrix} $$
Order of matrix E is 3-by-2
$$ F = \begin {bmatrix} 2 \\ \end{bmatrix} $$
Order of matrix F is 1-by-1
$$ G = \begin {bmatrix} 2 & 3 & 0 \\ 1 & 2 & 3 \\ 2 & 4 & 5 \\ \end{bmatrix} $$
Order of matrix G is 3-by-3
$$ H = \begin {bmatrix} 2 & 3 & 4 \\ 1 & 0 & 6 \\ \end{bmatrix} $$
Order of matrix H is 2-by-3
Question 2. Which of the following matrices are equal?
$ A = \begin {bmatrix} 3 \\ \end{bmatrix}, $ $ B = \begin {bmatrix} 3 & 5 \\ \end{bmatrix}, $ $ C = \begin {bmatrix} 5 – 2 \\ \end{bmatrix}, $ $ D = \begin {bmatrix} 5 & 3 \\ \end{bmatrix}, $ $ E = \begin {bmatrix} 4 & 0 \\ 6 & 2 \\ \end{bmatrix}, $ $ F = \begin {bmatrix} 2 \\ 6 \\ \end{bmatrix}, $ $ G = \begin {bmatrix} 3 – 1 \\ 3 + 3 \\ \end{bmatrix}, $ $ H = \begin {bmatrix} 4 & 0 \\ 6 & 2 \\ \end{bmatrix}, $ $ I= \begin {bmatrix} 3 & 3 + 2 \\ \end{bmatrix}, $ $ J = \begin {bmatrix} 2 + 2 & 2 – 2 \\ 2 + 4 & 2 + 0 \\ \end{bmatrix} $
Solution:
The matrices A and C are equal as the order of matrix A = order of matrix C and the corresponding elements of both matrices are equal.
The matrices B and I are equal as the order of matrix B = order of matrix I and the corresponding elements of both matrices are equal.
The matrices E, H and J are equal as the order of matrix E = order of matrix H = order of matrix J and the corresponding elements of these three matrices are equal.
The matrices F and G are equal as the order of matrix F = order of matrix G and the corresponding elements of both matrices are equal.
Question 3. Find the values of a, b, c and d which satisfy the matrix equation.
$ \begin {bmatrix} a + c & a + 2b \\ c – 1 & 4d – 6 \\ \end{bmatrix} = \begin {bmatrix} 0 & -7 \\ 3 & 2d \\ \end{bmatrix} $
Solution:
As the matrices at both sides of given equation are equal so their corresponding elements must be equal. Therefore,
$ a + c = 0 \;\;\;\;\; (1) $
$ a + 2b = -7 \;\;\;\;\; (2) $
$ c – 1 = 3 \;\;\;\;\; (3) $
$ 4d – 6 = 2d \;\;\;\;\; (4) $
From equation (3), we have,
[highlight]$ c = 4 $[/highlight]
By putting $ c = 4 $ in equation (1), we have
[highlight]$ a = -4 $[/highlight]
Now putting $ a = -4 $ in equation (2), we have
$ -4 + 2b = -7 \;\;\;\;\; (2) $
$ \Rightarrow 2b = 4 – 7 $
$ \Rightarrow 2b = -3 $
[highlight]$ \Rightarrow b = {-3 \over 2} $[/highlight]
From equation (4), we have,
$ 4d – 2d = 6 $
$ \Rightarrow 2d = 6 $
[highlight]$ \Rightarrow d = 3 $[/highlight]
Related



You must be logged in to post a comment.