Question 1. Write the following quadratic equations in the standard form and point out pure quadratic equations. $ \pmb{ (i). \;\;\;\;\; (x + 7) (x − 3) = -7} $ Solution: The given quadratic equation is $$ (x + 7) (x − 3) = -7 \;\;\;\;\; (i) $$ Multiplying the expressions $ (x + 7)…
In this method, write the quadratic equation in the standard form as ax2 + bx + c = 0 (i) If two numbers r and s can be found for the equation (i) such that r + s = b and rs = ac then ax2 + bx + c can be factorized into two…
To solve a quadratic equation by the method of completing square is illustrated through the following examples. Example Solve the equation x2 − 3x − 4 = 0 by completing square. Solution: x2 − 3x − 4 = 0 (i) Shifting constant term −4 to the right, we have x2 − 3x = 4 …
To find the solution set of a quadratic equation, following methods are used: factorization completing square use of quadratic formula
An equation of 2nd degree is called quadratic equation. In more detail, the quadratic equation is an equation, which contains the square of the unknown (variable) quantity, but no higher power. General or standard form of a quadratic equation: A 2nd degree equation in one variable x of the form as below, where a ≠ 0…
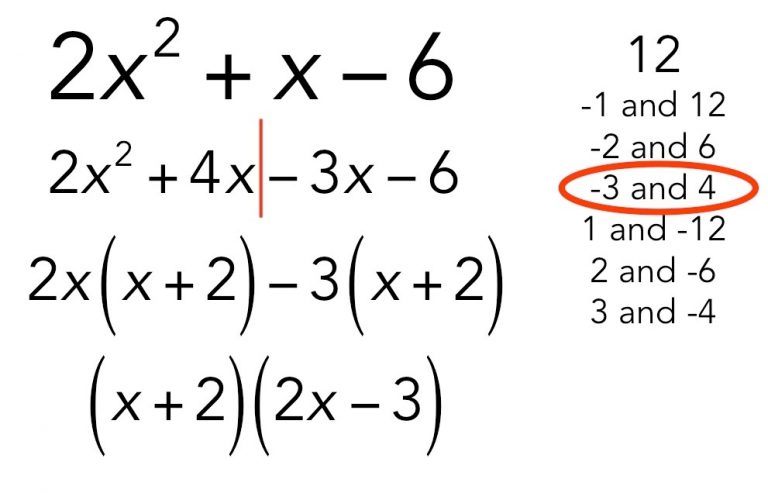
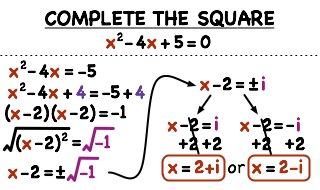
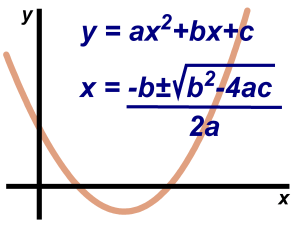
You must be logged in to post a comment.