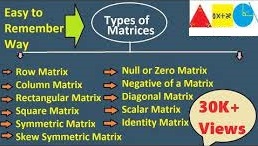
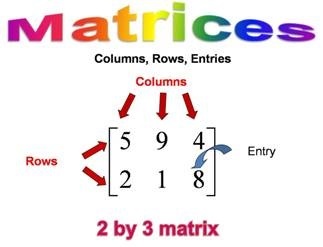
Properties, Laws and Formulae
Real Numbers Properties of Real Numbers For any real numbers a, b and c; $$ \forall \; a, b \in R \quad \Rightarrow \quad a+b \in R $$ $$ \forall \; a, b \in R \quad \Rightarrow \quad a . b \in R $$ $$ (a + b) + c = a + (b +…



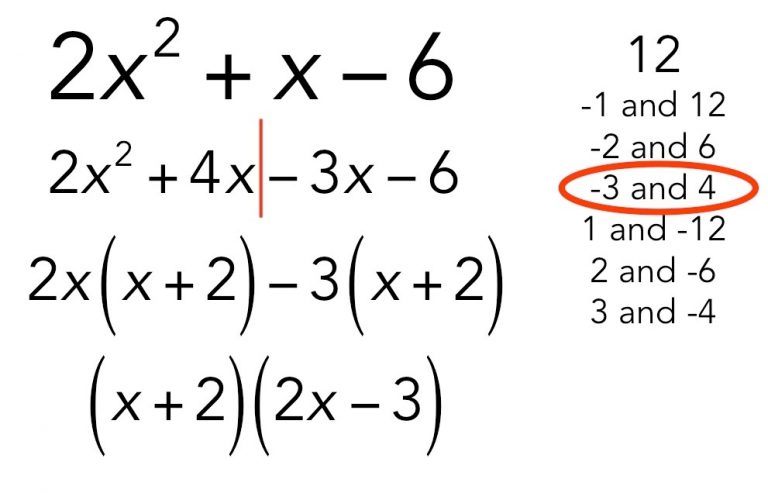
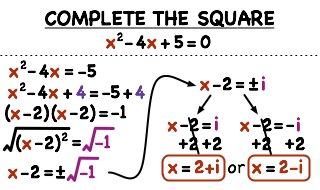
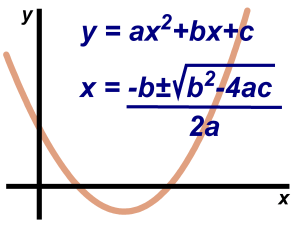
You must be logged in to post a comment.