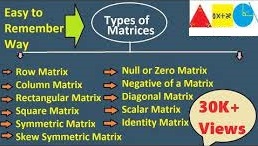
Types of Matrices

Row Matrix

A matrix is called a row matrix, if it has only one row.

e.g., the matrix $ M =  \begin {bmatrix} 2 & -1 & 7 \\ \end{bmatrix} $ is a row matrix of order 1-by-3 and $ N =  \begin {bmatrix} 1 & -1 \\ \end{bmatrix} $ is a row matrix of order 1-by-2.

Column Matrix

A matrix is called a column matrix, if it has only one column.

e.g., $ M =  \begin {bmatrix} 1 \\ 0 \\ \end{bmatrix} $ and $ N =  \begin {bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} $ are column matrices of order 2-by-1 and 3-by-1 respectively. 

Rectangular Matrix

A matrix M is called rectangular if, the number of rows of M is not equal to the number of columns of M.

e.g,. $ A =  \begin {bmatrix} 1 & 2 \\ 1 & 1 \\ 2 & 3 \\ \end{bmatrix}; $ $ B =  \begin {bmatrix} a & b & c \\ d & e & f \\ \end{bmatrix}; $ $ C =  \begin {bmatrix} 1 & 2 & 3 \\ \end{bmatrix}; $ and $ D =  \begin {bmatrix} 7 \\ 8 \\ 0 \\ \end{bmatrix} $ are all rectangular matrices. The order of A is 3-by-2, the order of B is 2-by-3, the order of C is 1-by-3 and order of D is 3-by-1, which indicates that in each matrix  the number of rows ≠ the number of columns.

Square Matrix

A matrix is called a square matrix, if its number of rows is equal to its number of columns.

e.g., $ A =  \begin {bmatrix} 2 & -1 \\ 0 & 3 \\ \end{bmatrix}; $ $ B =  \begin {bmatrix} 1 & 2 & 3 \\ -1 & 0 & -2 \\ 0 & 1 & 3 \\ \end{bmatrix} $ and $ C =  \begin {bmatrix} 3 \\ \end{bmatrix} $ are square matrices of orders, 2-by-2, 3-by-3 and 1-by-1 respectively.

Null or Zero Matrix

A matrix M is called a null or zero matrix, if each of its entries is 0.

e.g., $ \begin {bmatrix} 0 & 0 \\ 0 & 0 \\ \end{bmatrix}, $ $ \begin {bmatrix} 0 & 0 \\ \end{bmatrix}, $ $ \begin {bmatrix} 0 \\ 0 \\ \end{bmatrix}, $ $ \begin {bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} $ and $ \begin {bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} $ are null matrices of orders 2-by-2, 1-by-2, 2-by-1, 2-by-3 and 3-by-3 respectively.
Note that null matrix is represented by O.