Solution of Quadratic Equation by factorization
In this method, write the quadratic equation in the standard form as
ax2 + bx + c = 0 (i)
If two numbers r and s can be found for the equation (i) such that
r + s = b and rs = ac
then ax2 + bx + c can be factorized into two linear factors.
Example
Solve the quadratic equation 3x2 − 6x = x + 20 by factorization.
Solution:
3x2 − 6x = x + 20 (i)
The standard form of (i) is
3x2 − 7x − 20 = 0 (ii)
Here a = 3, b = −7, c = −20
and ac = 3 × (−20) = −60
As −12 + 5 = −7 and −12 × 5 = −60, so
the equation (ii) can be written as
3x2 − 12x + 5x − 20 = 0
or 3x (x − 4) + 5 (x − 4) = 0
⇒ (x − 4) (3x + 5) = 0
Either x − 4 = 0 or 3x + 5 = 0
x = 4 or 3x = −5 ⇒ x = −5⁄3
∴ x = −5⁄3, 4 are the solutions of the given equation.
Thus, the solution set is {−5⁄3, 4}.
Activity:
Factorize x2 − x − 2 = 0.
Solution:
x2 − x − 2 = 0 (i)
Here a = 1, b = −1, c = −2
and ac = 1 × (−2) = −2
As −2 + 1 = −1 and −2 × 1 = −2, so
the equation (i) can be written as
x2 − 2x + x − 2 = 0
or x (x − 2) + 1 (x − 2) = 0
⇒ (x − 2) (x + 1) = 0
∴ (x − 2), (x + 1) are factors of the given equation.
Example
Solve 5x2 = 30x by factorization.
Solution:
5x2 = 30x
Remember that cancelling of x on both sides of 5x2 = 30x means the loss of one root, i.e., x = 0
5x2 − 30x = 0 (i)
The equation (i) is factorized as
5x (x − 6) = 0
Either 5x = 0 or x − 6 = 0 ⇒ x = 0 or x = 6
∴ x = 0, 6 are the roots of the given equation.
Thus, the solution set is {0, 6}.

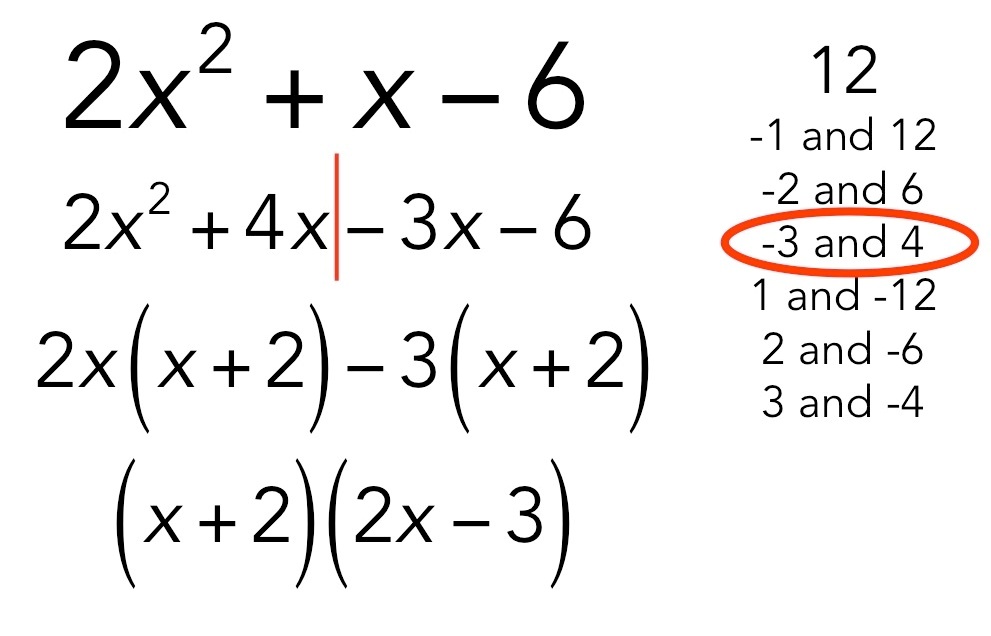


You must be logged in to post a comment.