Solution of Quadratic Equation by Completing Square
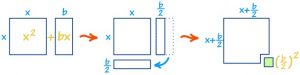
To solve a quadratic equation by the method of completing square is illustrated through the following examples.
Example
Solve the equation x2 − 3x − 4 = 0 by completing square.
Solution:
x2 − 3x − 4 = 0 (i)
Shifting constant term −4 to the right, we have
x2 − 3x = 4 (ii)
Adding the square of 1⁄2 × coefficient of x, that is,
(−3⁄2)2 on both sides of equation (ii), we get
x2 − 3x + (−3/2)2 = 4 + (−3/2)2 (ii)
As x2 − 3x + (−3/2)2 = x2 − 1⁄2 × x × 3⁄2 + (−3⁄2)2 = (x−3⁄2)2, so we have
(x−3⁄2)2 = 4 + 9⁄4 = 4 + (16 + 9)/4
(x−3⁄2)2 = 25⁄4
Taking square root of both sides of the above equation,
√(x−3⁄2)2 = ±√(25⁄4)
⇒ x−3⁄2 = ± 5⁄2 or x = 3⁄2 ± 5⁄2
Either x = 3⁄2 + 5⁄2 = (3 + 5)/2 = 8⁄2 = 4 or x = 3⁄2 − 5⁄2 = (3 – 5)/2 = −2⁄2 = −1
∴ 4, −1 are the roots of the given equation.
Thus, the solution set is {−1, 4}.
Example
Solve the equation 2x2 − 5x − 3 = 0 by completing square.
Solution:
2x2 − 5x − 3 = 0
Dividing each term by 2, to make coefficient of x2 equal to 1.
x2 − (5/2)x – 3/2 = 0
Remember that for our convenience, we make the co-efficient of x2 equal to 1 in the method of completing square.
Shifting constant term −3/2 to the right, we have
x2 − 5⁄2 x = 3/2 (i)
Adding the square of 1/2 × coefficient of x , that is, (1/2 × −5/2)2 = (−5/4)2 on both sides of equation (i), we get
x2 − 5⁄2 x + (−5/4)2 = 3/2 + (−5/4)2, that is,
(x − 5/4)2 = 3/2 + 25/16 = (24 + 25)/16
(x − 5/4)2 = 49/16
Taking square root of both sides of the above equation,
√(x− 5/4)2 = ±√(49/16)
⇒ x− 5/4 = ± 7/4 or x = 5/4 ± 7/4
Either x = 5/4 + 7/4 = (5 + 7)/4 = 12/4 = 3
or x = 5/4 − 7/4 = (5 − 7)/4 = − 2/4 = − 1/2
∴ 3, −1/2 are the roots of the given equation
Thus, the solution set is {−1/2, 3}.

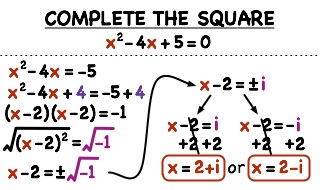



You must be logged in to post a comment.