Solution of Quadratic Equations
To find the solution set of a quadratic equation, following methods are used:
- factorization
- completing square
- use of quadratic formula
To find the solution set of a quadratic equation, following methods are used:
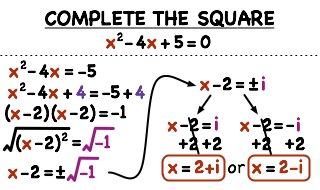
To solve a quadratic equation by the method of completing square is illustrated through the following examples. Example Solve the equation x2 − 3x − 4 = 0 by completing square. Solution: x2 − 3x − 4 = 0 (i) Shifting constant term −4 to the right, we have x2 − 3x = 4 …

Chinese New Year is a holiday that celebrates the beginning of a new year according to the according to the Chinese lunar calendar. It is considered to be one of the most important holidays for Chinese families. The holiday is celebrated with big family gatherings, gift giving, the eating of symbolic foods and display and…

The last couple of years have been a long bumpy ride for me, as they have for everyone of my age. The experiences might be different but everyone has gone through many of the same “teenage” circumstances as I have done. All of them have dealt with them in their own way. As a personal…

Real Numbers Properties of Real Numbers For any real numbers a, b and c; $$ \forall \; a, b \in R \quad \Rightarrow \quad a+b \in R $$ $$ \forall \; a, b \in R \quad \Rightarrow \quad a . b \in R $$ $$ (a + b) + c = a + (b +…

Generally, we presume that most chemical and physical changes proceed to completion. A complete reaction is one in which all reactants have been converted into products. However, most chemical reactions do not go to completion because products react themselves to form the reactants. As a result, after sometime no further change takes place. Quantities of…
You must be logged in to post a comment.