Exercise 1.1 (Math 10)
Question 1. Write the following quadratic equations in the standard form and point out pure quadratic equations. $ \pmb{ (i). \;\;\;\;\; (x + 7) (x − 3) = -7} $ Solution: The given quadratic equation is $$ (x + 7) (x − 3) = -7 \;\;\;\;\; (i) $$ Multiplying the expressions $ (x + 7)…


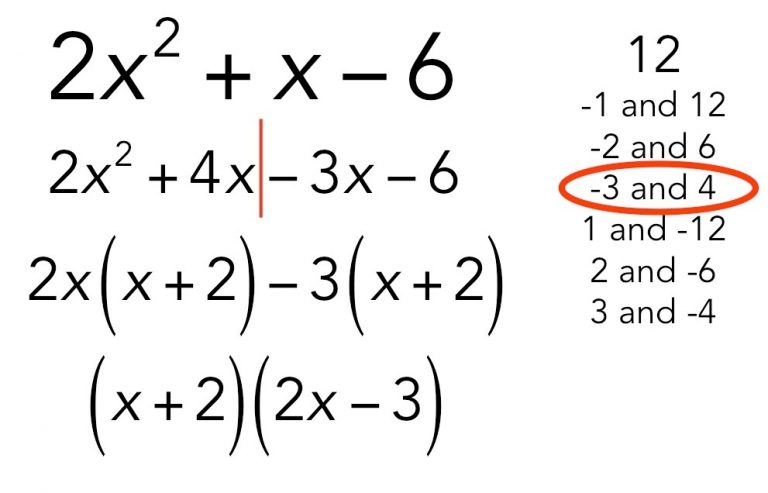
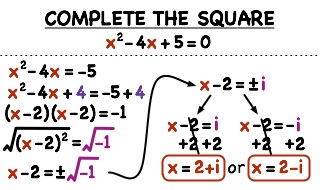
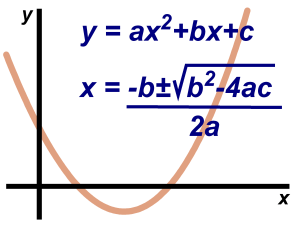
You must be logged in to post a comment.