Simple Harmonic Motion and Waves
A body is said to be vibrating if it moves back and forth or to and fro about a point. Another term for vibration is oscillation. A special kind of vibratory or oscillatory motion is called the Simple Harmonic Motion (SHM).
Simple Harmonic Motion (SHM)
A body is said to be executing Simple Harmonic Motion (SHM) if acceleration of the body is
- proportional to displacement of the body, and
- always directed towards mean position of the body
Some examples of Simple Harmonic Motion (SHM) are:
- the motion of mass attached to a spring on a horizontal frictionless surface
- the motion of a ball placed in a bowl
- the motion of a bob attached to a string
Motion of mass attached to a spring
One of the simplest types of oscillatory motion is that of horizontal mass-spring system as shown in the figure below:
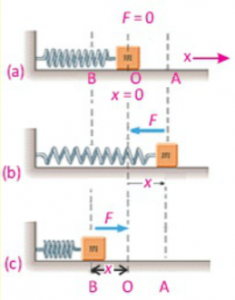
If the spring is stretched or compressed through a small displacement x from its mean position, it exerts a force F on the mass. According to Hooke’s law this force is directly proportional to the change in length x of the spring i.e.,
$$ F = \, – k x \;\;\;\;\;\; (i) $$
where x is the displacement of the mass from its mean position O, and k is a constant called the spring constant defined as:
$$ k = \,- {F \over x} $$
The value of k is a measure of the stiffness of the spring. Stiff springs have large value of k and soft springs have small value of k.
As F = m a
Using equation (i),
$$ – kx = ma $$
Therefore, $$ k = \, – {ma \over x} $$
or $$ a = \, – {k \over m} x $$
$$ a ∝ − x \;\;\;\;\;\; (ii) $$
It means that the acceleration of a mass attached to a spring is directly proportional to its displacement from the mean position. Hence, the horizontal motion of a mass-spring system is an example of simple harmonic motion.
The negative sign in equation (i) means that the force exerted by the spring is always directed opposite to the displacement of the mass. Because the spring force always acts towards the mean position, it is sometimes called a restoring force (a restoring force always pushes or pulls the object performing oscillatory motion towards the mean position).
Initially the mass m is at rest in mean position O and the resultant force on the mass is zero (figure – a). Suppose the mass is pulled through a distance x up to extreme position A and then released (figure – b). The restoring force exerted by the spring on the mass will pull it towards the mean position O. Due to the restoring force the mass moves back, towards the mean position O. The magnitude of the restoring force decreases with the distance from the mean position and becomes zero at O. However, the mass gains speed as it moves towards the mean position and its speed becomes maximum at O. Due to inertia the mass does not stop at the mean position O but continues its motion and reaches the extreme position B.
As the mass moves from the mean position O to the extreme position B, the restoring force acting on it towards the mean position steadily increases in strength. Hence the speed of the mass decreases as it moves towards the extreme position B. The mass finally comes briefly to rest at the extreme position B (figure – c). Ultimately the mass returns to the mean position due to the restoring force.
This process is repeated, and the mass continues to oscillate back and forth about the mean position O. Such motion of a mass attached to a spring on a horizontal frictionless surface is known as Simple Harmonic Motion (SHM).
The time period T of the simple harmonic motion of a mass ‘m’ attached to a spring is given by the following equation:
$$ T = 2\pi \sqrt{m \over k}$$





You must be logged in to post a comment.