Sets
A set is a collection of well defined distinct objects or symbols.
Well defined objects mean that the objects possess a property that enables one to determine whether a given object is in the collection or not. For example, a set cannot consist of elements like moral values, concepts, evils or virtues.
Element of a set
Each object in the set is called an element or member of the set. Symbolically it is represented by the symbol, ∈. For example, if an object x is an element of a set A then it is represented as x ∈ A and it is read as “x belongs to A”. Similarly, if x is not an element of A then it is represented as x ∉ A and is read as “x does not belong to A”.
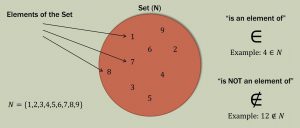
Tabular Form of writing a set
A set X with 10 elements (counting numbers from 1 to 10) in tabular form can be written as:
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Descriptive Form of writing a set
The same set in the descriptive form can be written as:
X is a set of 1st ten natural numbers.
Empty Set
A set that contains no elements. It is also called null set.
It is denoted by φ (phi) or { }.
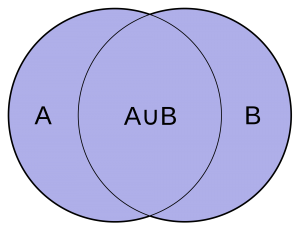
Union of two sets
If A and B are any two sets, the union of A and B is the set consisting of all elements in set A or in set B (or in both A and B). It is denoted by A ∪ B.
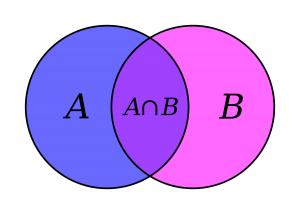
Intersection of two sets
If A and B are any two sets, the intersection of A and B is the set consisting of all elements common to both A and B. It is denoted by A ∩ B.
Example of Union and Intersection of two sets
A = {0, 1, 2}
B = {0, 3, 4}
A ∪ B = {0, 1, 2, 3, 4}
A ∩ B = {0}
Note: The order of listing the elements of a set does not matter.



You must be logged in to post a comment.